Links to other parts of the series:
I thought it might be fun to do a little series on implementing common data structures.
For the first one, I decided to do a HashMap.
What I thought would be a pretty short post ballooned into 3 posts,
as I learned about benchmarking, SIMD, and unsafe Rust.
In this post and the next two, I’ll walk through 6 iterations on a HashMap,
starting from a super basic map made out of other standard library containers,
and building up to a simplified version of Google’s Swiss Tables.
(Hashbrown, the Rust standard library’s map, is also based on Swiss Tables.)
All the code from this post is available here.
Let’s dive in!
Table of Contents
- Review of hashmap concepts
- Roadmap for the series
- Safe, naive map with separate chaining
- Safe, naive map with quadratic probing
- Footnotes
Review of hashmap concepts
First, we’ll lay the foundation for the rest of the post with a bit of review and terminology. I’ll go fast here since I assume the reader likely understands this better than I do.
I referred to the CLRS book when writing this part; see that book (or your favorite algorithms book) for a more in-depth treatment.
A hashmap is a collection that stores key-value pairs (k, v) and supports (on average) O(1) lookup, insert, and delete.
Here is what our basic API will look like (in Rust):
pub struct HashMap<K, V> { .. }
impl<K, V> HashMap<K, V>
where
K: PartialEq + Eq + core::hash::Hash,
{
// Lookup a key in the map.
// Named "get" instead of "lookup" to match Rust standard library.
pub fn get(&self, k: &K) -> Option<&V> { .. }
// Insert a key-value pair into the map.
// If the key was already present, returns the old value.
pub fn insert(&mut self, k: K, v: V) -> Option<V> { .. }
// Remove an item from the map.
// If the item was present, return its value.
// Named "remove" instead of "delete" to match Rust standard library.
pub fn remove(&mut self, k: &K) -> Option<V> { .. }
}
I’ll refer to these three operations (lookup, insertion, deletion) as the “map operations.” Of the three, lookup is the most fundamental, and so when it comes to discussing the underlying algorithms, I’ll usually just describe lookup. Once you have lookup, insertion and deletion are simple (conceptually at least):
- Insert key
kand valuev: Lookupkin the map. If present, replace its current value withv. Otherwise, insert a new entry with keykand valuev. - Delete key
k: Lookupkin the map, and if present, remove its entry.
Hash tables are generally implemented with a heap-allocated array that holds key-value pairs.
Each position in the array is called a “bucket”.
In Rust, we might represent this storage array as a Box<[Option<(K, V)>]>.1
(Sorta. We’ll see soon that this is a little too simple.)
The secret sauce behind the O(1) operations is the use of a hash function fn hash(k: &K) -> u64, which turns the key into a number.
The key can be any type that is hashable (i.e., implements Rust’s Hash trait).
The key’s bucket in the backing array is chosen to be its hash value modulo the array length.
Since calculating the hash and indexing into the array are both O(1), this means that lookup is O(1).
Great! Except… what if two items end up in the same bucket?
Collisions
When two items end up in the same bucket, it’s called a “hash collision”. There are two primary ways of dealing with collisions: separate chaining and open addressing.
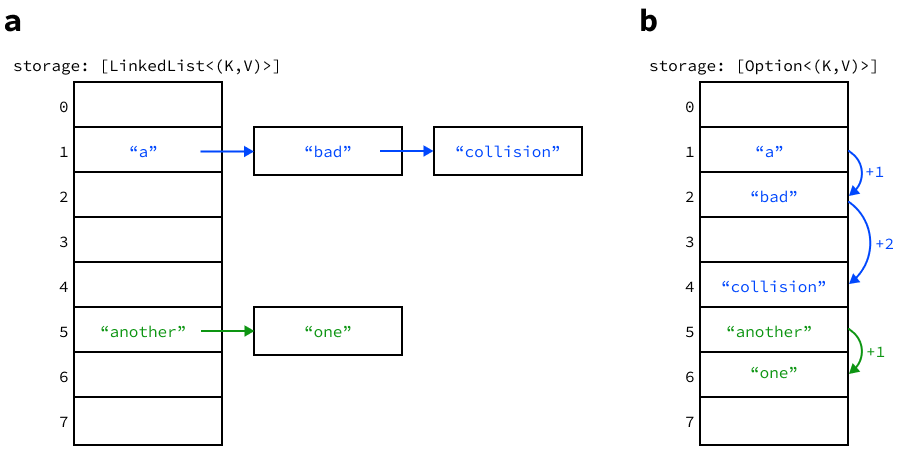
["a", "bad", "collision"] and ["another", "one"] have hashed to the same buckets.
For simplicity, the map values are not shown.
Separate chaining
In chaining, each bucket holds the head of a linked list
(in Rust, LinkedList<(K, V)>) instead of a single item (K, V).
For all three map operations, we find the bucket for the requested key k and then walk down the linked list at that location, looking for a list node whose key matches k.
If we hit the end of the list, then we know that k is not in the map.
This strategy is simple to implement and has the advantage that the list nodes can be easily moved around when resizing the map.
In languages that aren’t as strict as Rust, this means that we can hand out pointers to the nodes that won’t be invalidated when the map is resized—i.e., the nodes have “pointer stability”.
For example, C++11 guarantees pointer stability for std::unordered_map, which essentially requires implementations to use chaining.
Unfortunately, chaining is generally not very fast due to poor memory locality—in fact, the relatively poor performance of std::unordered_map is attributed to the use of chaining (see e.g., this article from Facebook).
Since the list nodes are unlikely to be adjacent in memory, walking down a chain may cause multiple cache misses.
This can be somewhat improved by using a Vec<(K, V)> (which holds its memory contiguously) instead of a linked list,
though at the cost of losing pointer stability.
(To keep the map operations efficient, we will want to avoid long chains anyway, which reduces the advantages of using a Vec. More on this below in the load factor section.)
Open addressing
An alterative to chaining is open addressing.
In open addressing, we keep the backing storage as an array, Box<[Option<(K, V)>]>.
Hash collisions are dealt with by checking a predetermined sequence (“probe sequence”) of new positions relative to the initial bucket.
For all three of insertion, lookup, and deletion, this means following the probe sequence until we find a bucket whose key matches the query key, or an empty bucket if the key isn’t in the map.
Probing is more cache-friendly than chaining, since we only need to pull one big chunk of contiguous memory (the backing storage) into the cache. However, one can see that probing may actually make things slower depending on the exact probe sequence, as we’ve seemingly introduced a bunch more collisions.
In linear probing, the probe sequence just steps by a certain number of buckets (usually 1) on each iteration.
As an example, suppose we are trying to do an insertion, and our initial bucket (index = 10) is full.
In linear probing, we’ll check buckets 11, 12, 13, ... looking for an empty bucket, wrapping around once we reach the end of the array.
Linear probing is simple to implement, but can cause problems due to clustering. Clustering can cause collisions to snowball as long probe chains cover more and more slots over time, leading to coupling (or correlation, or whatever you want to call it) between the probe sequences for nearby buckets.
An alternative is quadratic probing, where the step size in the probe sequence increases quadratically. Probably the most common choice (and the one we’ll use here) is increasing the step size by 1 on each step, which will hit every bucket if the number of buckets is a power of 2 (see e.g., CLRS or Wikipedia). This still results in clustering (“secondary clustering”), though it tends to be less bad than what happens for linear probing.
Load factor
In the preceeding discussion, we’ve implicitly assumed that collisions are rare, which is necessary for the operations to remain (on average) O(1).
Otherwise, for both chaining and probing, the runtime of the hashmap operations will degrade to O(N)
(where N is the number of items in the map).
With chaining, the linked lists will start to get long, on the order of N.
With probing, the probe sequences will eventually need to visit every bucket in the backing storage.
These effects are typically quantified in terms of a “load factor”, which is the number of items in the map divided by the total number of buckets. Typically, one would set a maximum load factor (maybe in the range of 0.7 to 0.9?) beyond which the map is resized. Resizing is implemented by allocating a new backing array (usually a factor of 2 larger than the current storage) and re-inserting all of the items into the new array.
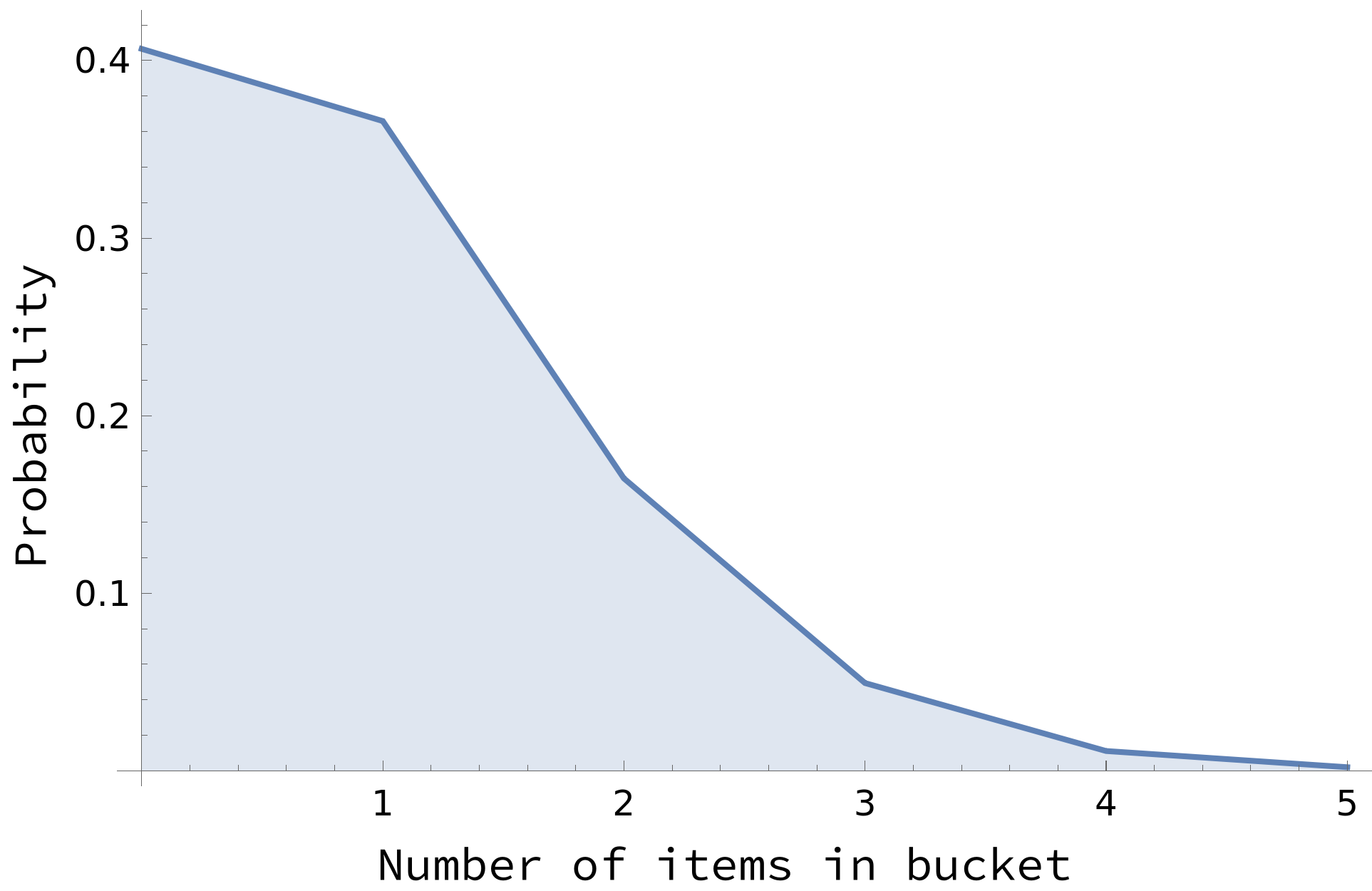
Note that for chaining, the load factor is roughly the expected number of items in a chain. Keeping a load factor below 1 means that chains are typically not longer than a single element. We can make a more quantitative estimate by approximating the number of items in a single bucket as having a Poisson distribution2, with the Poisson parameter λ given by the load factor. As shown in the graph below, for a load factor of 0.9 the bucket has more than 1 item only about 25% of the time.
(Note: this analysis is more complicated for the open addressing scheme, since the probe sequence introduces correlations between the buckets.)
Roadmap for the series
Between this post and the next two, I’ll go through 6 iterations on a custom hashmap, which will include a decent amount of code. I like putting lots of code snippets, especially for the earlier maps, since it emphasizes how simple the implementation can be. (And for the harder parts, it’s nice to show which parts were particularly tricky.)
However, I recognize that lots of code snippets can become a slog to read through, so I’d like to first discuss some high-level points up front. If you’re not interested in seeing the code details, you can treat this section as a tldr.
Outline
Here is a brief description of each of the six maps:
-
Separate chaining (safe Rust). This uses an array of
std::collections::LinkedListas the backing storage. -
Open addressing with quadratic probing (safe Rust). This uses an array of
Bucket<K, V>as the backing storage, whereBucketis an enum with 3 states:empty,tombstone, orFull(K, V). TheTombstonevariant is needed to mark deleted items; when searching for an item, we don’t stop probing until we reachEmpty. -
Open addressing with Swiss Table-style metadata (safe Rust). Following Google’s Swiss Tables hashmap, we store additional metadata that consists of one byte per bucket. The metadata byte contains a control bit (is the bucket full or empty/deleted?) and a 7-bit hash of the key. When probing for a key
k, we probe first on the densely-packed metadata, which allows us to filter out lots of candidates based on the 7-bit hash. The real Swiss Tables implementation also uses SIMD instructions to parallelize probing, which is not implemented (yet). -
Unsafe version of #3 using
MaybeUninit. Our previous maps all have the unfortunate limitation that the backing storage memory needs to be fully initialized (a tradeoff of using safe Rust). This can become expensive when resizing a large map, as we have to zero out each bucket. However, the fact that we have metadata actually allows us to never look at a bucket unless it’s full! This lets us leave any empty buckets uninitialized in memory, at the cost of a little bit ofunsafecode. -
SIMD probing version of #4. Following Swiss Tables, we can actually do the probing in a (somewhat) parallel fashion by using SIMD instructions. Instead of probing individual metadata entries, we’ll form groups of 16 metadata entries to probe together with SIMD.
-
Using the
AllocatorAPI to put metadata and storage in the same allocation. Finally, we’ll try some very unsafe things to put the metadata and storage in the same allocation. This was my first experience writingunsafeRust and I ignored some details (like unwind safety), so this implementation is surely unsound by the Rust community’s standards. That being said, I did my best to check withmirithat the code works as expected for the narrow subset of situations that I tested and benchmarked.
Each post in the series will cover two of these maps.
A few early conclusions
More conclusions to follow in the next posts, but for now:
-
If you just need a pretty fast map,
unsafeis totally not necessary. Even a very naive design like my first map is only 2-3x slower thanstd’s hashmap on the map operations, according to my benchmarks. -
Speaking of which: Benchmarks are hard. I spent much more time trying to understand the results of my benchmarks than actually writing my hashmap implementations. To be totally transparent, I’m still not convinced that my benchmarks are all correct.
-
More appreciation for the engineering that goes into the standard library abstractions. Parts 2 and 3 dip into some
unsafecode, and only really scratch the surface of how gnarlyunsafecan get. It does help a lot thatstd’s code is not so complicated as to be totally incomprehensible (partially because hashbrown’s code has good docs). -
Consider boxing your data if it’s big. With a better understanding of how std’s
HashMapworks, it’s clear that you should consider boxing your values if they are large (> 10’s of pointers?).
Safe, naive map with separate chaining
Boilerplate
I started a new project called cornedbeef (get it? corned beef hash? haha), with modules for each design iteration of the hashmap.
Here’s what the directory looks like for the first two maps:
cornedbeef/
- src/
- lib.rs
- first.rs
- second.rs
- benches/
- bench.rs
- Cargo.toml
The benches/ directory will eventually be used for writing benchmarks, but let’s ignore that for now.
Here’s lib.rs:
// lib.rs
use core::hash::{BuildHasher, Hasher};
use std::collections::hash_map::DefaultHasher;
pub mod first; // Our first map lives here
pub mod second;
pub mod third;
pub mod fourth;
/// Hash builder for std's default hasher.
pub type DefaultHashBuilder = core::hash::BuildHasherDefault<DefaultHasher>;
/// Convenience function for hashing a key.
fn make_hash<S, K>(build_hasher: &S, key: &K) -> u64
where
S: BuildHasher,
K: core::hash::Hash,
{
let mut hasher = build_hasher.build_hasher();
key.hash(&mut hasher);
hasher.finish()
}
/// Choose an actual capacity from the requested one.
fn fix_capacity(capacity: usize) -> usize {
match capacity {
0 => 0,
x if x < 16 => 16,
x => x.next_power_of_two(),
}
}
/// Calculate the remainder using bitwise AND.
/// The modulus must be a power of 2 for this to work.
#[inline(always)]
fn fast_rem(n: usize, modulus_power_of_two: usize) -> usize {
n & (modulus_power_of_two - 1)
}
These utilities are in the top-level module since they’ll be common to all of our hashmap implementations.
First, we have some boilerplate for our hash function (DefaultHashBuilder) and to calculate hashes (make_hash).
I basically copied this part from hashbrown.
We’ll use the Rust standard library’s hash function (std::collections::hash_map::DefaultHasher) in order to make a fair comparison later with std’s HashMap.
We also have a function fix_capacity to calculate the initial capacity of the map (how big the backing storage is) from a user-provided value.
We use this to ensure that the storage size is always a power of 2, which is required for the later maps that use quadratic probing.
If the initial capacity is 0, we don’t want to allocate anything until the first element is added to the map.
We also set the smallest nonzero capacity to be 16 to avoid a bunch of small allocations early on3.
If the requested capacity is 16 or larger, we round up the capacity to the nearest power of 2.
Finally, we have a fast_rem function to calculate the remainder mod n for n = 2^k.
Since we’ll maintain a power-of-2 storage size, we can use fast_rem to efficiently calculate the bucket index from the hash.
See the box below for details.
Aside: Performance and
fast_rem:Since we’re iterating on the map design, I didn’t spend much time on optimizations. However, I did find a huge difference (>20% improvement in the benchmarks) by using bitwise AND instead of
usize::rem_euclidto calculate the modulus by the number of buckets.(This optimization works because
n_bucketsis always a power of two,x & (n_buckets - 1) = x mod n_buckets.)This optimization is especially important for the maps that use probing, since they need to calculate the current index
mod n_bucketsat each step of the probe sequence to properly wrap around the storage array. To make a fair comparison, I decided to include this optimization in all of the maps.
Implementation
Let’s move on to the actual implementation of the map (first.rs).
Here’s what the Map looks like:
// first.rs
//! A naive map with separate chaining.
use core::hash::{BuildHasher, Hash};
use std::collections::LinkedList;
use crate::{fast_rem, fix_capacity, make_hash, DefaultHashBuilder};
/// A hashmap with separate chaining.
#[derive(Debug, Clone)]
pub struct Map<K, V, S: BuildHasher = DefaultHashBuilder> {
hasher: S,
n_items: usize,
storage: Box<[LinkedList<(K, V)>]>,
}
// continued...
Our Map is pretty literally what we’d previously described for a map with chaining:
we have a struct member storage that holds a heap-allocated array4 of LinkedList<(K, V)>.
We additionally hold the hasher (in case we want to customize the hash function later on) and the number of items currently in the map (n_items).
Let us start with some static methods to create an instance of Map.
Following std’s HashMap, we’ll provide a new method that doesn’t allocate, and a with_capacity method that initially allocates enough space to fit the requested number of elements:
// first.rs
// ...continued
impl<K, V> Map<K, V> {
pub fn new() -> Self {
Self::with_capacity(0)
}
pub fn with_capacity(capacity: usize) -> Self {
let capacity = fix_capacity(capacity);
let storage = (0..capacity)
.map(|_| LinkedList::new())
.collect();
Self {
hasher: DefaultHashBuilder::default(),
n_items: 0,
storage,
}
}
}
impl<K, V> Default for Map<K, V> {
fn default() -> Self {
Self::new()
}
}
// continued...
Note that Map::with_capacity uses the fix_capacity function we defined earlier in lib.rs.
The with_capacity method will be particularly helpful during benchmarking to understand the various costs involved with insertion (i.e., the cost of probing vs resizing the map).
Next, we’ll define some basic methods:
// first.rs
// ...continued
impl<K, V> Map<K, V> {
pub fn len(&self) -> usize {
self.n_items
}
pub fn is_empty(&self) -> bool {
self.n_items == 0
}
#[inline]
pub(crate) fn n_buckets(&self) -> usize {
self.storage.len()
}
}
// continued...
These are pretty straightforward, so let’s implement the rest of the map operations.
To match std’s HashMap, we’ll have methods get and get_mut for lookup, as well as insert and remove methods.
To implement get and get_mut, we find the bucket for the given key and then walk down the list stored at that bucket.
If we find the key we’re looking for, we return a reference to its value, otherwise we return none.
Pretty simple right? Here’s what it looks like in code:
// first.rs
// ...continued
impl<K, V> Map<K, V>
where
K: PartialEq + Eq + Hash,
{
/// Hash a key to its bucket.
fn bucket_index(&self, k: &K) -> usize {
let hash = make_hash(&self.hasher, k);
fast_rem(hash as usize, self.n_buckets())
}
/// Lookup key `k`.
pub fn get(&self, k: &K) -> Option<&V> {
let index = self.bucket_index(k);
for (kk, vv) in self.storage[index].iter() {
if kk == k {
return Some(vv);
}
}
None
}
/// Lookup (mutable) key `k`.
pub fn get_mut(&mut self, k: &K) -> Option<&mut V> {
let index = self.bucket_index(k);
for (kk, vv) in self.storage[index].iter_mut() {
if kk == k {
return Some(vv);
}
}
None
}
}
// continued...
(A quick note on the trait bounds on the impl block (K: PartialEq + Eq + Hash):
If you haven’t used Rust, this just means that we’ve only implemented these methods for key types k that are hashable and have an equality operation (otherwise, we wouldn’t be able to check k == kk above).)
As you can see, this is a pretty literal translation of what we described earlier for lookup in a chaining scheme.
The same pattern is used to implement insert and remove, so I won’t show the full code for those methods.
One slight wrinkle is that we may need to resize the map before inserting, as shown in the snippet below:
// first.rs
// ...continued
impl<K, V> Map<K, V>
where
K: PartialEq + Eq + Hash,
{
/// Insert key `k` with value `v` into the map.
/// If `k` was already present, returns `Some(old_value)`.
/// Else returns `None`.
pub fn insert(&mut self, k: K, v: V) -> Option<V> {
if self.needs_resize() {
self.resize();
}
self._insert(k, v)
}
/// Actually implements the insert!
fn _insert(&mut self, k: K, v: V) -> Option<V> { ... }
/// Removes key `k` from the map.
/// If `k` was present in the map, returns `Some(value)`.
pub fn remove(&mut self, k: &K) -> Option<V> { ... }
}
// continued...
Finally, I’ll show the code for resizing the map.
First, the needs_resize function.
If we have zero buckets, then we definitely need to resize the map.
Otherwise, we compare the current load factor against the maximum load factor, which we’ve chosen (somewhat arbitrarily) to be 7/8.
Similar to our earlier choice of initial nonzero capacity (16), we’d probably want to benchmark this to determine the optimal load factor for a realistic workload.
// first.rs
// ...continued
impl<K, V> Map<K, V>
where
K: PartialEq + Eq + Hash,
{
/// Returns `true` if we need to resize the map.
fn needs_resize(&self) -> bool {
// Using a load factor of 7/8.
self.n_buckets() == 0 || ((self.n_items * 8) / self.n_buckets()) > 7
}
}
// continued...
Now, to actually resize the map.
The actual resize function calculates the new capacity and initializes an empty storage array.
We then walk through the old storage array and rehash our keys to buckets in the new storage.
// first.rs
// ...continued
impl<K, V> Map<K, V>
where
K: PartialEq + Eq + Hash,
{
fn resize(&mut self) {
// Calculate the new capacity.
let capacity = match self.n_buckets() {
0 => 16,
x => x * 2,
};
// Set `self.storage` to a new array.
let new_storage = (0..capacity)
.map(|_| LinkedList::new())
.collect();
let old_storage = std::mem::replace(&mut self.storage, new_storage);
self.n_items = 0;
// Move nodes from `old_storage` to `self.storage`.
for mut bucket in Vec::from(old_storage).into_iter() {
while !bucket.is_empty() {
// We want to reuse the nodes, so we can't pop them.
let tail = bucket.split_off(1);
let mut head = bucket;
bucket = tail;
let (k, _) = head.front().unwrap();
let index = self.bucket_index(k);
self.storage[index].append(&mut head);
self.n_items += 1;
}
}
}
}
// continued...
This final loop is a little bit ugly because we want to reuse our list nodes instead of destroying them and then allocating them again,
which necessitates5 using split_off and append
instead of simply pop_front.
Setting up tests
Finally, we need some tests!
I’ll show them all here once.
The same tests will be used for all of the various Map versions.
These first two tests check that we can insert, lookup, and delete:
#[test]
fn insert() {
let mut map = Map::new();
for i in 0..1000 {
map.insert(i, i);
}
assert_eq!(map.len(), 1000);
for i in 0..1000 {
assert_eq!(map.get(&i), Some(&i));
}
}
#[test]
fn remove() {
let mut map = Map::new();
for i in 0..1000 {
map.insert(i, i);
}
assert_eq!(map.len(), 1000);
for i in 0..1000 {
assert_eq!(map.remove(&i), Some(i));
}
assert_eq!(map.len(), 0);
}
We should also check that we don’t get any false positives when doing a lookup:
#[test]
fn miss() {
let mut map = Map::new();
for i in 0..1000 {
map.insert(i, i);
}
assert_eq!(map.len(), 1000);
for i in 1000..2000 {
assert!(map.get(&i).is_none());
}
assert_eq!(map.len(), 1000);
}
We should also check that resizing is working as we expect.
This is done by inserting items, removing them, and then re-inserting the same items,
while keeping track of how map.len() and map.n_buckets() are changing:
#[test]
fn remove_and_reinsert() {
let mut map = Map::new();
let range = 0..1000;
for i in range.clone() {
map.insert(i, i);
}
assert_eq!(map.len(), 1000);
let buckets = map.n_buckets();
for i in range.clone() {
assert_eq!(map.remove(&i), Some(i));
}
assert_eq!(map.len(), 0);
assert_eq!(buckets, map.n_buckets());
for i in range {
map.insert(i, i);
}
assert_eq!(map.len(), 1000);
assert_eq!(buckets, map.n_buckets());
}
Finally, here are few extra tests that will come in handy for later maps that use unsafe:
#[test]
fn empty_map_doesnt_allocate() {
let map = Map::<usize, usize>::new();
assert_eq!(0, std::mem::size_of_val(&*map.storage));
}
#[test]
fn drop_empty_map() {
let _ = $map::<String, String>::new();
}
#[test]
fn insert_nontrivial_drop() {
let mut map = $map::new();
let items = (0..1000).map(|i| (i.to_string(), i.to_string()));
for (k, v) in items {
map.insert(k, v);
}
assert_eq!(map.len(), 1000);
}
#[test]
fn insert_borrowed_data() {
let items = (0..1000)
.map(|i| (i.to_string(), i.to_string()))
.collect::<Vec<_>>();
let mut map = $map::new();
for (k, v) in &items {
map.insert(k, v);
}
assert_eq!(map.len(), 1000);
}
In my actual code, I wrapped this up into a macro_rules! that takes the map type as the input.
This makes it easy to add the same test suite for each new design iteration without code duplication.
Setting up benchmarks
I used criterion.rs to set up my benchmarks.
To start, I added the following to my Cargo.toml:
[dev-dependencies]
criterion = "0.4"
[[bench]]
name = "bench"
harness = false
This sets cargo bench to look at benches/bench.rs.
I also exported first::Map in the crate root by adding the following in my lib.rs:
pub use first::Map as CbHashMap;
Here is a brief description of each benchmark (N = 10⁵):
new: Create an empty map of a given capacity (either 0 orN16-byte items).drop: Run the destructor for a map withNitems (K = usize,V = String). For types with trivial drop,StdHashMapcan takes some shortcuts, but I didn’t think that was a super fair comparison with the initial maps that don’t useunsafe.insert_grow_seq: Starting from an empty map withcapacity = 0, insert keys 0, 1, …,N - 1.insert_grow_random: Starting from an empty map withcapacity = 0, insertNkeys from a pseudorandom number generator.insert_reserved_random: Same asinsert_grow_random, but the map has an initial capacity ofN(so no resizes are needed).lookup: Starting from a map withNitems (pseudorandomusizes), look up each of those items.lookup_string: Starting from a map withNitems (pseudorandomusizeconverted toStrings), look up each of those items. This is intended to test the performance when equality comparisons are expensive (like for strings, as opposed to integers).lookup_miss: Starting from a map withNitems (pseudorandomusizes), look upNitems that aren’t in the map.remove: Starting from a map withNitems (pseudorandomusizes), remove each item.
The insert, lookup, and remove benchmarks were tested using K = usize and either V = usize (payload = 8 bytes) or V = [usize; 8] (payload = 64 bytes).
These value sizes were chosen based on Matt Kulukundis’s CppCon talk on swiss tables, which shows some benchmarks using 4 byte and 64 byte values.
For exact details on how the benchmarks are run, please see the repo.
Aside: Benchmarking mistakes
Instead of showing the full benchmarking code here, I wanted to briefly mention a few problems I ran into:
Forgetting to clone the data:
Criterion runs repeated benchmarks to get good statistics on the timing. Many of the simplest examples use
Bencher::iterto run the benchmark, which takes a closure with the routine to run.In my first attempts, I initialized the hashmap and then let the closure capture it, which led to incorrect results. Here’s a simplified example to clarify what I mean:
// Create a new hashmap. let mut map = Map::new(); // Add 100_000 items to it. for i in 0..100_000 { map.insert(i, i); } // Declare the benchmark c.bench_function("remove", |b| { // Here is the routine to run: b.iter(|| { // Remove the 100_000 items. for i in 0..100_000 { // `black_box` keeps the compiler // from removing dead code. black_box(map.remove(&i)); } }) });Can you spot the problem? Since the inner closure captures
mapby mutable reference, the first run of the benchmark removes all the items, and all subsequent runs see an empty map!Instead, I needed to use
Bencher::iter_batched, which takes another closure to run setup code. Here’s what the new version looks like:// ... // Declare the benchmark c.bench_function("remove", |b| { b.iter_batched( // Setup code for each iteration: // Make a deep copy of the map! || map.clone(), // The actual code to benchmark: |mut map| { // Remove the 100_000 items. for i in 0..100_000 { black_box(map.remove(&i)); } }, BatchSize::PerIteration, ) });Dominated by drop:
Actually, the above code is still not quite right. Destructing (in Rust terms, “dropping”) the map was pretty slow, especially for
first::map, and ended up dominating the time of the benchmarks.To fix this, I used
Bencher::iter_batched_ref, which does not consume themap(in contrast toBencher::iter_batched), and thus avoids runningdropinside of the benchmark.
Aside (Edit 4/10/2023): More benchmarking mistakes
When writing Part 3a on SIMD probing, I found another mistake with the benchmarks. The symptom was that the speed of individual benchmarks depended on which other benchmarks were also present in the final binary. For more discussion of the fix, please see that post.
Speed comparison with std
These were run locally on my machine:
- OS: Fedora 37
- CPU: Intel i7-10750H
- RAM: 32 GB
Here are the results6:
| Benchmark | std | first::Map | Ratio |
|---|---|---|---|
| new (capacity: 0) | 7 ns | 5 ns | 0.7 |
| new (capacity: 10⁵ 16-byte items) | 2.1 μs | 126 μs | 60 |
| drop (10⁵ items) | 1.5 ms | 4.5 ms | 3.0 |
| insert_grow_seq (payload: 8 bytes) | 3.7 ms | 9.2 ms | 2.2 |
| insert_grow_seq (64 bytes) | 4.5 ms | 10.6 ms | 2.4 |
| insert_grow_random (8 bytes) | 3.7 ms | 9.1 ms | 2.5 |
| insert_grow_random (64 bytes) | 4.7 ms | 10.4 ms | 2.2 |
| insert_reserved_random (8 bytes) | 2.0 ms | 4.6 ms | 2.3 |
| insert_reserved_random (64 bytes) | 2.6 ms | 5.3 ms | 2.0 |
| lookup (8 bytes) | 2.1 ms | 2.5 ms | 1.2 |
| lookup (64 bytes) | 2.3 ms | 2.7 ms | 1.2 |
| lookup_string (8 bytes) | 4.1 ms | 4.6 ms | 1.1 |
| lookup_string (64 bytes) | 7.3 ms | 5.3 ms | 0.7 |
| lookup_miss (8 bytes) | 1.8 ms | 2.6 ms | 1.4 |
| lookup_miss (64 bytes) | 1.8 ms | 2.9 ms | 1.6 |
| remove (8 bytes) | 4.5 ms | 7.5 ms | 1.7 |
| remove (64 bytes) | 5.8 ms | 11.6 ms | 2.0 |
As you can see, this map is about 2x slower than std’s on the map operations.
As we noted before, the main problem is likely poor locality from putting the items on the heap, leading to poor cache performance. Since open addressing tends to be more cache-friendly, our next map will be based on a quadratic probing scheme.
Safe, naive map with quadratic probing
Here’s the declaration of our second map:
// second.rs
//! A naive map with open addressing and quadratic probing.
#[derive(Debug, Clone)]
pub struct Map<K, V, S: BuildHasher = DefaultHashBuilder> {
hasher: S,
n_items: usize, // Number of live items
n_occupied: usize, // Number of occupied buckets
storage: Box<[Bucket<K, V>]>,
}
// continued...
Two things are different from first::Map.
First, we’ve added a new struct member n_occupied, which is apparently different somehow from n_items (more on this in a bit).
Second, storage now holds a slice of Bucket<K, V>, where before it held LinkedList<(K, V)>.
Here’s the definition of Bucket:
// second.rs
// ...continued
pub enum Bucket<K, V> {
Empty,
Tombstone,
Full(K, V),
}
// continued...
Bucket is an enum with three states: Empty, Tombstone, and Full(K, V).
It’s pretty easy to guess what an Empty or Full bucket means.
Even better, we can state this in terms of the probing algorithm:
if we reach an Empty bucket during the probe sequence for k, then k is not in the map.
This is great, except for when we start to remove items.
If we remove k and set its bucket to Empty, then we’ve rendered all items after k in the probe sequence inaccessible!
This is where Bucket::Tombstone comes in.
Instead of setting k’s bucket to Empty, we set it to Tombstone, which means: “There used to be an item here, but it was removed. Keep probing!”
While we’re here, let’s define some convenience methods on Bucket.
The following methods just allow easy access to the contents of the Bucket if it is Full:
// second.rs
// ...continued
impl<K, V> Bucket<K, V> {
pub fn into_inner(self) -> Option<(K, V)> {
if let Self::Full(k, v) = self {
Some((k, v))
} else {
None
}
}
pub fn as_inner(&self) -> Option<(&K, &V)> {
if let Self::Full(k, v) = self {
Some((k, v))
} else {
None
}
}
pub fn as_mut(&mut self) -> Option<(&mut K, &mut V)> {
if let Self::Full(k, v) = self {
Some((k, v))
} else {
None
}
}
}
// continued...
Now that we understand Bucket::Tombstone, we can explain the distinction between “live” items (map.n_items) and “occupied buckets” (map.n_occupied).
Obviously, the number of live items is important for implementing standard methods like self.len().
For resizing the map, however, what really matters is the number of live items plus the number of tombstones—i.e., the number of occupied buckets (map.n_occupied).
Thus, our needs_resize method becomes the following:
// second.rs
// ...continued
impl<K, V> Map<K, V>
where
K: PartialEq + Eq + Hash,
{
fn needs_resize(&self) -> bool {
// Using a load factor of 7/8.
// Important: we need to use n_occupied instead of n_items here!
self.n_buckets() == 0 || ((self.n_occupied * 8) / self.n_buckets()) > 7
}
}
// continued...
Implementing probing
The basic map operations all depend on probing for items in the map.
Let’s bundle all of this logic up into a common probe_find method.
First, we define an enum ProbeResult that contains the two possible end states when probing for key k:
Empty(i): We reached an empty bucket at indexi, so we conclude thatkis not in the map.Full(i): We foundkin the bucket at indexi.
There’s no end state corresponding to Bucket::Tombstone—remember, Tombstone always tells us to keep probing.
// second.rs
// ...continued
enum ProbeResult {
Empty(usize),
Full(usize),
}
// continued...
The probe algorithm is simple:
- First, hash our key
kto find the starting bucket index (current). - At each step of the probe sequence, we find the new
currentindex by addingstep(modulon_buckets).stepincrements by 1 on each step of the probe sequence, resulting in quadratic probing. Recall from before that this sequence is guaranteed to hit every bucket ifn_bucketsis a power of 2. - If the current bucket is empty, return
ProbeResult::Empty(current). - If the current bucket is full and its key equals
k, returnProbeResult::Full(current). - If we exhaust the probe sequence, we’ll panic with
unreachable!(). This would mean that there are no empty buckets instorage, and thus we’ve violated our maximum load factor (a bug!).
Here’s what this looks like in code:
// second.rs
// ...continued
impl<K, V> Map<K, V>
where
K: PartialEq + Eq + Hash,
{
fn probe_find(&self, k: &K) -> ProbeResult {
let mut current = self.bucket_index(k);
for step in 0..self.n_buckets() {
current = fast_rem(current + step, self.n_buckets());
match &self.storage[current] {
Bucket::Empty => return ProbeResult::Empty(current),
Bucket::Full(kk, _) if kk == k => {
return ProbeResult::Full(current);
}
// Keep probing.
Bucket::Tombstone | Bucket::Full(..) => {}
}
}
unreachable!("backing storage is full, we didn't resize correctly")
}
}
// continued...
Not too bad right?
Implementing map operations
With probe_find in hand, the other map operations are pretty simple.
get and get_mut are pretty self-explanatory:
We simply probe for k and if we find it, return a reference to its value.
// second.rs
// ...continued
impl<K, V> Map<K, V>
where
K: PartialEq + Eq + Hash,
{
pub fn get(&self, k: &K) -> Option<&V> {
match self.probe_find(k) {
ProbeResult::Empty(_) => None,
ProbeResult::Full(index) =>
self.storage[index].as_inner().map(|(_, v)| v),
}
}
pub fn get_mut(&mut self, k: &K) -> Option<&mut V> {
match self.probe_find(k) {
ProbeResult::Empty(_) => None,
ProbeResult::Full(index) =>
self.storage[index].as_mut().map(|(_, v)| v),
}
}
}
// continued...
remove is just slightly more complicated.
We probe for k and if we find it, we replace its bucket in storage with a Tombstone.
Using std::mem::replace allows us to hold onto the old contents of the bucket and return the value for k.
It’s important that we decrement self.n_items but not self.n_occupied, since we’re leaving behind a tombstone!
// second.rs
// ...continued
impl<K, V> Map<K, V>
where
K: PartialEq + Eq + Hash,
{
pub fn remove(&mut self, k: &K) -> Option<V> {
match self.probe_find(k) {
ProbeResult::Empty(_) => None,
ProbeResult::Full(index) => {
// Replace the full bucket with a tombstone.
let old_bucket = std::mem::replace(
&mut self.storage[index],
Bucket::Tombstone
);
// Important to decrement only `n_items`
// and not `n_occupied` here,
// since we're leaving a tombstone.
self.n_items -= 1;
old_bucket.into_inner().map(|(_, v)| v)
}
}
}
}
// continued...
To implement _insert, we again probe for k.
If we find an empty bucket, then we need to insert (k, v) into storage
at that bucket7 and increment both of self.n_items and self.n_occupied.
If we find a full bucket, we just replace its value with the new value.
// second.rs
// ...continued
impl<K, V> Map<K, V>
where
K: PartialEq + Eq + Hash,
{
pub fn insert(&mut self, k: K, v: V) -> Option<V> {
if self.needs_resize() {
self.resize();
}
self._insert(k, v)
}
fn _insert(&mut self, k: K, v: V) -> Option<V> {
match self.probe_find(&k) {
// We need to add `k` to the map.
ProbeResult::Empty(index) => {
self.storage[index] = Bucket::Full(k, v);
self.n_items += 1;
self.n_occupied += 1;
None
}
// `k` is in the map.
// We need to replace its old value.
ProbeResult::Full(index) => {
let (_, vv) = self.storage[index].as_mut().unwrap();
Some(std::mem::replace(vv, v))
}
}
}
}
// continued...
Finally, here is the implementation of resize:
// second.rs
// ...continued
impl<K, V> Map<K, V>
where
K: PartialEq + Eq + Hash,
{
fn resize(&mut self) {
// Calculate the new capacity.
let capacity = match self.n_buckets() {
0 => 16,
x => x * 2,
};
// Set `self.storage` to a new array.
let new_storage = (0..capacity)
.map(|_| Bucket::Empty)
.collect::<Vec<_>>()
.into_boxed_slice();
let old_storage = std::mem::replace(&mut self.storage, new_storage);
self.n_items = 0;
self.n_occupied = 0;
// Move nodes from `old_storage` to `self.storage`.
for bucket in Vec::from(old_storage).into_iter() {
if let Some((k, v)) = bucket.into_inner() {
self._insert(k, v);
}
}
}
}
This is actually a fair bit simpler than the LinkedList version, where we had to do something funky to preserve the list nodes.
For this version, we can just iterate through the old storage array and just _insert every item into the new storage.
Here, it helps to have _insert be a separate function from insert, as it allows us avoid checking needs_resize unneccesarily.
Speed comparison with std
I ran the same exact benchmarks as described in the previous section.
Here are the results (numbers are now given as a ratio of runtime with std’s runtime):
| Benchmark | first | second |
|---|---|---|
| new (capacity: 0) | 0.7 | 0.5 |
| new (capacity: 10⁵ 16-byte items) | 60 | 27 |
| drop (10⁵ items) | 3.0 | 1.1 |
| insert_grow_seq (payload: 8 bytes) | 2.2 | 2.1 |
| insert_grow_seq (64 bytes) | 2.4 | 2.6 |
| insert_grow_random (8 bytes) | 2.5 | 2.1 |
| insert_grow_random (64 bytes) | 2.2 | 2.5 |
| insert_reserved_random (8 bytes) | 2.3 | 1.5 |
| insert_reserved_random (64 bytes) | 2.0 | 1.6 |
| lookup (8 bytes) | 1.2 | 1.2 |
| lookup (64 bytes) | 1.2 | 1.5 |
| lookup_string (8 bytes) | 1.1 | 1.3 |
| lookup_string (64 bytes) | 0.7 | 1.5 |
| lookup_miss (8 bytes) | 1.4 | 2.0 |
| lookup_miss (64 bytes) | 1.6 | 3.0 |
| remove (8 bytes) | 1.7 | 0.7 |
| remove (64 bytes) | 2.0 | 0.6 |
Here are a few observations that probably make sense:
- Drop: much faster for
second::Map, about on par withstd’s map. - Many operations are a bit faster in the new map, but performance regressed for large payloads across the board (except
insert_reserved). This could be because keeping such large values in the storage array makes probing less cache-friendly, since we have to travel a long way in memory to find the next key to compare. In other words, the stride of the access pattern is long, leading to worse locality. Swiss tables uses densely-packed metadata (1 byte per bucket) to get around this problem, which we will implement in the next iteration of the map. - On the other hand,
insert_reserveddid improve in the new map, even for large payloads, suggesting that growing the map still incurs a significant performance penalty.
And a few confusing observations:
- The “miss” variants regressed a lot, I’m not sure why these would necessarily be worse than
first::Map. - I don’t know why
removeappears to now be faster thanstd’s map… I’m not inclined to trust that result though. IF this result is correct, it might be because hashbrown has to do a bit more work to decide if it should place a tombstone (owing to its more complicated probing scheme). See this blog post by Gankra for a description.
To address these problems, we’ll add some metadata in the next iteration of the map to make probing more efficient in Part 2.
Footnotes
If you are unfamiliar with Rust, this is a heap-allocated (Box’ed) slice ([T]) of optional key-value pairs (Option<(K, V)>).
Optional means that each bucket in the array could either be full (holding a Some((K, V))) or empty (holding None).
This estimate should be pretty accurate for a single bucket. Once we start to consider multiple buckets, there will be some correlations between buckets since the total number of items in the map is fixed.
The size 16 is pretty arbitrary, and should probably be checked by benchmarking a realistic program.
I used a Box<[T]> here instead of a Vec<T> because I think it’s a bit clearer.
The nice thing about Vec is that it handles resizing automatically for you, but we’ll want to handle resizing manually anyway.
Plus, we’ll never need Vec operations like push or pop.
It shouldn’t matter here,
but Box<[T]> is also slightly smaller (size of 2 pointers) than Vec<T> (size of 3 pointers).
There’s actually an experimental method (LinkedList::remove) that does this a little more cleanly, but I wanted to stick to stable Rust for this first iteration.
Criterion reports statistics over 100 runs, but the standard deviation was usually quite small (< 5%) so I just used the mean in the table.
I also noticed fluctuations of ~10% between runs of cargo bench, which should probably be treated as an overall systematic error on the measurement.
This strategy is a little wasteful on memory, since buckets with a Tombstone are never used again (until the map is resized).
For simplicity, I chose to just waste the tombstone slots here, but this is actually not too hard to fix—we
could remember the first Tombstone we see and return its position if we reach an Empty bucket.
Interestingly, hashbrown (which uses a much more complicated probing scheme)
does a double-lookup to implement this.