Links to other parts of the series:

• Part 1: Intro and two naive maps
• Part 2: Swiss Table metadata and MaybeUninit
• Part 3b: Exception safety
• Part 3c: Resizing with SIMD

Welcome back to my series on writing a hashmap in Rust!

Please see Part 1 and Part 2 for an introduction. To recap:

• In Part 1, we wrote two simple hashmaps using separate chaining in a linked list (first::Map) and open addressing with quadratic probing (second::Map).
• In Part 2, we further improved the performance by incorporating metadata (modeled off of Google’s Swiss Tables map) and applying some unsafe optimizations.

In this post, we’ll apply another optimization used in Swiss Tables and Rust’s hashbrown: SIMD instructions to parallelize probing.

(Link to the repo.)

Table of Contents

1. Profiling and optimization
2. SIMD probing
3. Implementation
4. Speed comparison with std
5. Next steps: Allocator API
6. Footnotes

Profiling and optimization

As of now, this blog is mostly documenting my learning journey. Since I’m learning things as I go, this space isn’t primarily meant to be a resource to others—it’s more of a journal. As a result, many parts of this hash map series have not been presented in a very principled way.

The whole discussion about performance throughout the series is definitely one of these things. One might reasonably ask: “Why are we talking about low-level optimizations like SIMD when we haven’t even profiled the code?” … and… yeah, that’s a good point.

The answer is: because I didn’t really know how to. But if our optimizations are going to make any sense, we’d better figure it out!

In writing this post, I learned that CS has something called Amdahl’s law. Amdahl’s law is pretty intuitive—it basically says: focus on the hot spots. An incremental improvement in a procedure that’s a performance bottleneck is usually more impactful than a huge improvement in a procedure that’s rarely called (or already very fast).

So how do we figure out the hotspots? Profiling! In particular, we’ll use a tool called cargo-flamegraph to generate a flamegraph, which helps us to visualize the function call stack and see which procedures are taking the most CPU time.

To install, run cargo install flamegraph, which installs the cargo-flamegraph subcommand. Before taking any traces, we’ll need to add debug symbols to our release build:

# Cargo.toml
[profile.release]
debug = true

This needs to come before the [[bench]] section for it to work. We also need to have Linux’s perf command installed (or dtrace on other platforms).

Flamegraphs

Now that we’ve added debug symbols, we can start making flamegraphs. As a demo, we’ll profile the insert_grow_seq benchmark. To do this, we’ll comment out all the other benchmarks in our Criterion group, then run

$ cargo flamegraph --bench bench

This command produces the following flamegraph:

Flamegraphs represent runtime on the horizontal axis (wider boxes are functions that take more CPU time) and the call stack depth on the vertical axis.

The flamegraph above is pretty confusing, since there’s a lot of stuff happening inside of criterion. Opening this SVG in a browser allows us to zoom in on key areas, but here I’ll just throw some screenshots below to make this easier. Below is a zoom on the actual insert_grow_seq routine, showing the call stacks for fourth::Map::insert and std::collections::HashMap::insert side by side:

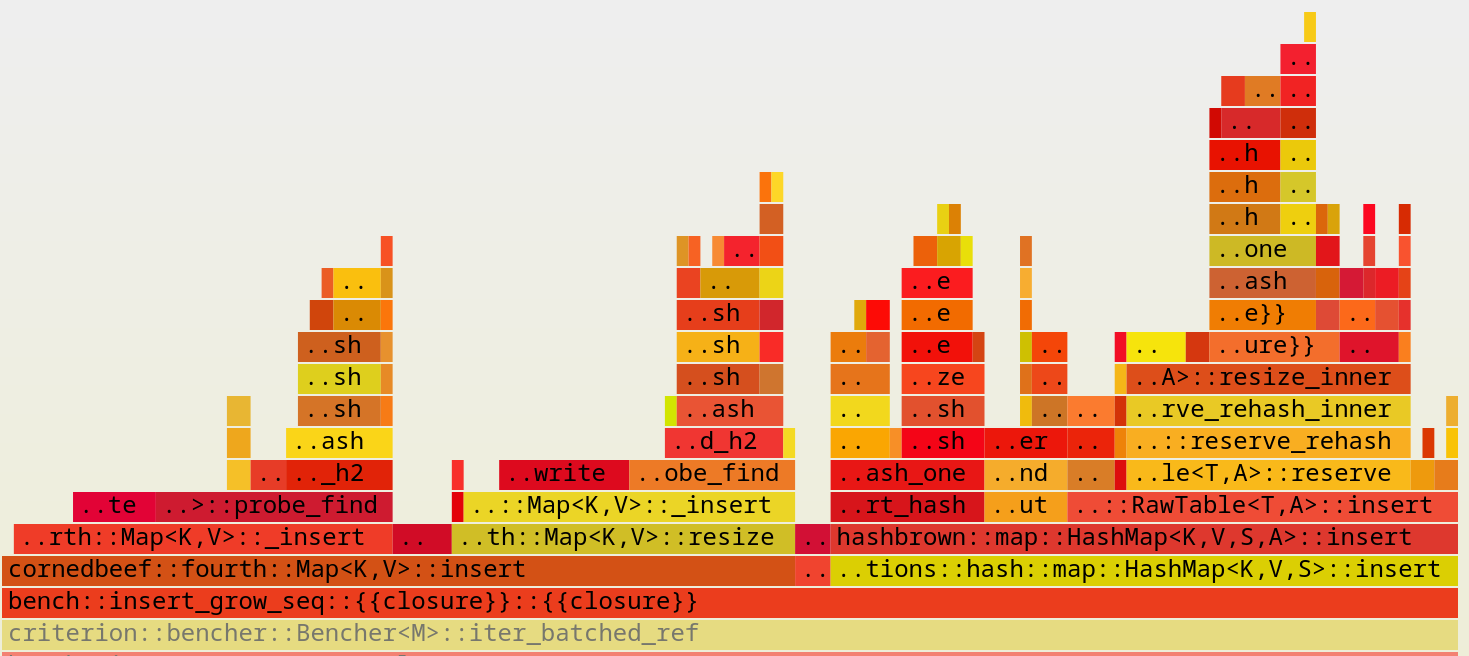
Still too much information! Let’s zoom in on fourth::Map’s probe_find routine:

It’s pretty hard to read like this (sorry!), but the above flamegraph does provide an important takeaway: there’s about 30% of the runtime that’s not in fast_rem or make_hash where we have room to improve things. That extra 30% of time is in our probing procedure, so it makes sense to try to improve that with SIMD.

In retrospect, this conclusion is pretty obvious—we’re using the same hashing procedure as std’s map, so of course the performance bottleneck must be elsewhere, and there’s not much happening in probe_find besides hashing and probing (duh). For a more complicated project, however, we might not have as much information a priori, and then profiling would be critical. In any case, it’s considered good practice to profile as a starting point for optimization, so I wanted to at least go through making a flamegraph here.

Long aside: Fixing the benchmarks

I mentioned earlier that I commented out some of the benchmarks to generate a simpler flamegraph. Doing this led to a surprising discovery: the speed of the benchmarks would change depending on which benchmarks were commented out!

This seemed obviously wrong—if the benchmarks are to be meaningful, they should at least be independent of which ones are enabled. Apparently, the way I’d initially written the benchmarks was giving the compiler some extra information, allowing it to further optimize things across different benchmarks.

After some investigation, I figured out that it was some of the setup code that I had factored out of the benchmarks. To explain this, I’ll show the signature for Bencher::iter_batched_ref, which I was using to run my benchmarks:

pub fn iter_batched_ref<I, O, S, R>(
    &mut self,
    setup: S,
    routine: R,
    size: BatchSize
)
where
    S: FnMut() -> I,
    R: FnMut(&mut I) -> O,

For the lookup and remove benchmarks, I was initially filling up a map outside of the benchmarking code, then cloning the map inside of the setup closure, and finally doing the map operations inside of the routine closure. However, it seemed like filling up the map outside of iter_batched_ref was giving the compiler more opportunities to optimize the inner workings of the hash map. Since not every benchmarks had the same initial steps, this would explain why the benchmark performance was changing depending on which ones were enabled.

Eventually, I moved all of the setup code (filling up the map, etc.) into the setup closure and added black_box around the map operations in setup, which seemed to fix the problem. Now, it seems that all the benchmarks give a consistent result whether they’re compiled and run individually or together in the same binary.¹

Here is an updated benchmark summary for the 4 maps so far, using the corrected benchmarking code. Again, all runtimes below are given as the ratio with std’s runtime.

Benchmark	first	second	third	fourth
new (capacity: 0)	0.8	0.7	1.3	0.7
new (capacity: 10⁵ 16-byte items)	52	40	42	1.0
drop (10⁵ items)	2.8	1.1	1.0	1.0
insert_grow_seq (payload: 8 bytes)	2.4	2.1	1.9	1.8
insert_grow_seq (64 bytes)	2.2	2.3	2.1	1.7
insert_grow_random (8 bytes)	2.4	2.0	1.9	1.8
insert_grow_random (64 bytes)	2.2	2.4	1.9	1.7
insert_reserved_random (8 bytes)	2.3	1.3	1.4	1.4
insert_reserved_random (64 bytes)	2.1	1.4	1.4	1.4
lookup (8 bytes)	1.3	1.3	1.3	1.2
lookup (64 bytes)	1.1	1.1	1.3	1.2
lookup_string (8 bytes)	1.2	1.3	1.0	0.9
lookup_string (64 bytes)	0.9	1.2	0.9	1.0
lookup_miss (8 bytes)	1.7	2.0	1.6	1.6
lookup_miss (64 bytes)	1.7	2.8	1.5	1.5
remove (8 bytes)	1.7	0.8	0.9	0.8
remove (64 bytes)	1.3	0.8	0.8	1.0

Some of the numbers have shifted a bit, but in general the trends are pretty similar to what they were before.

Okay! With that, we’re ready to move on to the SIMD probing scheme.

SIMD probing

In fifth::Map, we’ll use SIMD (specifically, SSE) instructions to parallelize probing. Here’s the idea: by grouping 16 adjacent metadata entries into a u8x16 vector, we can use SIMD instructions to query all 16 entries in a group with only a few instructions.

Brief introduction to SIMD

Note: This was my first time using SIMD. Corrections and clarifications are welcome!

SIMD stands for “single instruction, multiple data” and generally refers to operations on vectorized data. A vector data type is a slab of bits that is interpreted as a vector of some primitive type. For example, we might have a 256-bit vector type that is interpreted as 8 floats (f32). Each individual slot in the vector (each f32 in this example) is refered to as a lane. Following Rust’s std::simd, we’ll define f32x8 as the type of a vector with 8 f32 lanes, and similarly for other primitive numeric types (e.g., u8x16, u32x4, etc.).

The advantage of SIMD is that “vertical” operations between two vectors are extremely fast, often requiring only a single instruction. Vertical operations are those that are done lane-wise; for example, taking the vector sum:

In contrast, “horizontal” operations (for example, summing over the lanes of an f32x4 to obtain an f32) are generally slow.

Different architectures have different SIMD instructions. My laptop has an Intel i7 CPU so it has Intel SIMD extensions like SSE and AVX. These different SIMD instructions are partly distinguished by the size of their bitvectors; here we’ll primarily use SSE2 (128-bit vectors) for operations on u8x16. SIMD instructions operate on SIMD registers—e.g., xmm0, xmm1, … for SSE2. We’ll see these later when we look at the generated assembly.

We often don’t have to write SIMD explicitly since the compiler will apply “auto-vectorization” to generate SIMD instructions wherever possible. But if performance is really critical, one will usually want to have more control over vectorization to avoid being fully reliant on the compiler’s analysis. There are currently a few ways to go about this in Rust. First, we can use the actual SIMD intrinsics for our architecture, which are exposed through core::arch. This is the approach taken by hashbrown and Swiss tables (in C++). While this method gives the most control, it’s a bit intimidating for a SIMD beginner (like myself) and it’s not portable to other architectures. For this project, I’ll instead use the unstable portable SIMD standard library module (std::simd), which exposes cross-platform SIMD types and operations. The types in std::simd essentially wrap LLVM SIMD intrinsics, which are used in the compiler backend to describe SIMD in a cross-platform way.

In this post, we’ll be using just a few APIs from std::simd, which I’ll briefly introduce here. The main type in std::simd is Simd<T, LANES>, which represents a vector of T with number of lanes given by LANES. To make a new vector, we’ll use Simd::splat,

pub fn splat(value: T) -> Simd<T, LANES> 

which makes a new vector, with each lane containing value. We’ll also use the SimdPartialEq trait to take a lanewise ==,

fn simd_eq(self, other: Self) -> Self::Mask

This operation outputs a Mask<T, LANES>, which basically acts like a vector of bool. We’ll also use the ToBitMask to convert the mask into an unsigned integer—in this case, a u16, since we’ve got a 16-element mask.

Changing our probing strategy

At first, it seems like SIMD probing won’t fit with our current probing scheme. After all, using SIMD instructions makes the most sense when testing a block of adjacent metadata, but our quadratic probe sequence is constructed to avoid creating such blocks!

To get around this, both Swiss Tables and hashbrown split their metadata up into “Groups” of 16 adjacent elements, represented as a u8x16 vector. Then we can use SIMD to efficiently probe all the metadata entries in a single group, while still maintaining some robustness to clustering by doing quadratic probing on the groups.²

To actually probe a group with SIMD is pretty simple:

• First, convert the desired 16-element slice of metadata into a u8x16.
• Next, splat the value we want to check against into another u8x16. If we’re looking for empty entries, use value = Metadata::Empty(). If we’re looking for entries that match a given h2, use value = h2.
• Finally, compare the two vectors using SimdPartialEq. This outputs a mask where the true lanes correspond to the metadata entries that matched our query.

Alignment

Note that there’s a design choice to be made here: will we require that SIMD accesses are aligned? A SIMD type like u8x16 is actually aligned to [u8; 16], not u8, and aligned accesses are generally faster than unaligned ones. If we do require aligned accesses, then the group of an index i will be found by rounding i down to the nearest multiple of GROUP_SIZE = 16.

Interestingly, Swiss Tables and hashbrown make the opposite choice; each bucket is treated as the start of its own group. As a result, nearly every SIMD access is unaligned. However, as explained in Matt Kulukundis’s talk on Swiss Tables, this strategy actually gives more efficient probing and memory utilization. Here, I’ll just follow Swiss Tables and hashbrown, although I’d be curious to benchmark things later and see how the aligned version compares.

One important consequence of the unaligned approach is that we’ll have to add one extra group of metadata at the end of the array that replicates the first group, so we can still form a full group for the last few buckets. We’ll just need to remember this to keep this extra metadata in sync when updating.

Long aside: Viewing the generated assembly

When we get to implementing things, we’ll want to view the generated assembly so we can double-check that the compiler is actually emittting the SIMD instructions that we want.

To do this, I’m using the helpful tool cargo-show-asm. First, let’s install it by running cargo install cargo-show-asm. To get a list of available functions:

$ cargo asm --lib

which initially outputs only a single function:

cornedbeef::fix_capacity

That’s cool, but unfortunately fix_capacity isn’t really the most interesting or performance-critical function. (Recall from before that it essentially just rounds a user-provided capacity up to the nearest power of 2.)

There are two main reasons why functions won’t be visible to cargo asm: inlining and monomorphization.

Inlining: By definition, inlined functions don’t produce a function call in the generated assembly, making it impossible for cargo-asm to find their code. To fix this, we can simply ensure that functions aren’t inlined. As an example, we can put #[inline(never)] on our fast_rem function:

// lib.rs
#[inline(never)]
fn fast_rem(n: usize, modulus_power_of_two: usize) -> usize {
    n & modulus_power_of_two.saturating_sub(1)
}

Now fast_rem will show up in the output of cargo asm, and we can view its assembly:

$ cargo asm cornedbeef::fast_rem --lib
cornedbeef::fast_rem:
 xor     eax, eax
 sub     rsi, 1
 cmovae  rax, rsi
 and     rax, rdi
 ret

Aside: Comparison with usize::rem_euclid

If you recall from Part 1, I mentioned that using a bitmask instead of usize::rem_euclid gave about a 30% speed-up for all of the map operations. For fun, we can replace the inside of fast_rem with usize::rem_euclid to see the difference in the generated assembly:

$ cargo asm cornedbeef::fast_rem --lib
cornedbeef::fast_rem:
 test    rsi, rsi
 je      .LBB2_5
 mov     rax, rdi
 or      rax, rsi
 shr     rax, 32
 je      .LBB2_2
 mov     rax, rdi
 xor     edx, edx
 div     rsi
 mov     rax, rdx
 ret
.LBB2_2:
 mov     eax, edi
 xor     edx, edx
 div     esi
 mov     eax, edx
 ret
.LBB2_5:
 push    rax
 lea     rdi, [rip, +, str.0]
 lea     rdx, [rip, +, .L__unnamed_5]
 mov     esi, 57
 call    qword, ptr, [rip, +, _ZN4core9panicking5panic17hc46f6fd5636f0948E@GOTPCREL]
 ud2

Ouch… it’s a lot longer, there are branches, divisions, and a possible panic (in case of division by zero). I’m not great with assembly, but it seems pretty clear that this version will be slower that the bitmasking version.

Monomorphization: Besides inlining, monomorphization can also cause our functions to not show up in the emitted assembly. If you’re not familiar with the term, monomorphization refers to the process used by the compiler to generate code for generic functions. More precisely, monomorphization is a particular strategy for compiling a generic function fn foo<T>(..), in which a new version of foo<T> is produced and optimized for every concrete type T used in foo. Since our map type Map<K, V> is generic over the key and value types, this means that the compiler won’t generate assembly for any map operations unless we somehow call them in a public way.

To get around this limitation, we can add a simple public function to our library,

// lib.rs
/// This only exists to help us see the `Map` methods in the generated assembly.
pub fn get<'a>(map: &'a CbHashMap<usize, usize>, k: &'a usize) -> Option<&'a usize> {
    map.get(k)
}

This forces the compiler to generate code for Map<usize, usize>. Now, we can get some of the internal Map methods to show up in the assembly. For example, we’ll often want to look at the probe_find function, which is super hot since it’s called by all of the other map operations. The compiler has decided to inline this function, so we need to mark it #[inline(never)] to view its assembly. Then we get:

$ cargo asm "cornedbeef::fifth::Map<K,V>::probe_find" --lib
cornedbeef::fifth::Map<K,V>::probe_find:
 push    r15
 push    r14
 push    r12
 push    rbx
 sub     rsp, 56
(... etc. ...)

(I’ve only shown the first few lines here.)

Note that this assembly will be optimized for (K, V) = (usize, usize), and might be pretty different for other types (String). This is probably okay since we’ll generally be interested in optimizing the probing algorithm, which doesn’t depend on the types K and V.³

In the rest of the post, I’ll use these techniques to show the generated assembly in some spots. (Of course, disabling inlining can affect the performance a lot, so the benchmarks will always use the inlining directives shown in the Rust code snippets, even if I had to use #[inline(never)] to easily view the assembly.)

Implementation

(Link to the repo.)

Much of the implementation is similar to fourth::Map, except for the probing strategy implemented in the probe_find method.

Here’s the declaration of fifth::Map, which is identical to fourth::Map:

// fifth.rs

//! A Swiss Tables-inspired map with metadata.
//! Uses SSE instructions on the metadata.

use core::hash::{BuildHasher, Hash};
use std::marker::PhantomData;
use std::mem::MaybeUninit;

use crate::metadata::{self, Metadata};
use crate::sse::{self, GROUP_SIZE};
use crate::{fast_rem, fix_capacity, make_hash, DefaultHashBuilder};

pub struct Map<K, V, S: BuildHasher = DefaultHashBuilder> {
    hasher: S,
    n_items: usize,    // Number of live items
    n_occupied: usize, // Number of occupied buckets
    /// Safety: we maintain the following invariant:
    /// `self.storage[i]` is initialized whenever `self.metadata[i].is_value()`.
    storage: Box<[MaybeUninit<(K, V)>]>,
    /// Contains an extra `GROUP_SIZE` elements to avoid wrapping SIMD access
    metadata: Box<[Metadata]>,
    _ph: PhantomData<(K, V)>,
}

The implementations of Clone and Drop are the same as fourth::Map. We do make a small change to with_capacity to make sure we create the extra metadata group:

// fifth.rs

impl<K, V> Map<K, V> {
    pub fn with_capacity(capacity: usize) -> Self {
        let capacity = fix_capacity(capacity);

        let storage = Box::new_uninit_slice(capacity);

        // New: make extra metadata group at end if capacity > 0.
        // If capacity == 0, we still want to avoid allocating.
        let metadata = if capacity == 0 {
            Box::new([])
        } else {
            (0..(capacity + GROUP_SIZE))
                .map(|_| metadata::empty())
                .collect::<Vec<_>>()
                .into_boxed_slice()
        };

        Self {
            hasher: DefaultHashBuilder::default(),
            n_items: 0,
            n_occupied: 0,
            storage,
            metadata,
            _ph: PhantomData,
        }
    }
}

Here’s the new implementation of probe_find:

// fifth.rs

impl<K, V> Map<K, V>
where
    K: PartialEq + Eq + Hash,
{
    fn probe_find(&self, k: &K) -> ProbeResult {
        // Compute initial index and `h2` hash
        let (mut current, h2) = self.bucket_index_and_h2(k);

        // Quadratic probing
        for step in 0..self.n_buckets() {
            // Probe quadratically by Group instead of by individual buckets.
            current = fast_rem(current + step * GROUP_SIZE, self.n_buckets());
            let group = sse::Group::from_slice(&self.metadata[current..]);

            // First, check full buckets for items with matching `h2` hash.
            let candidates = sse::MaskIter::forward(group.to_candidates(h2));
            for i in candidates {
                let index = fast_rem(current + i, self.n_buckets());
                // SAFETY: `candidates` iterator only yields full buckets.
                let (kk, _) = unsafe { 
                    self.storage.get_unchecked(index).assume_init_ref() 
                };
                if kk == k {
                    return ProbeResult::Full(index);
                }
            }

            // If we've made it to here, our key isn't in this group.
            // Look for the first empty bucket.
            let empty = sse::find_first(group.to_empties());
            if let Some(i) = empty {
                let index = fast_rem(current + i, self.n_buckets());
                return ProbeResult::Empty(index, h2);
            }
        }
        ProbeResult::End
    }
}

That’s a lot of code, and a lot of new functions I haven’t introduced yet! Let’s walk through it:

• Start by computing the bucket index and the h2 hash like usual.
• Since we’re probing by groups instead of by buckets, increment the current index by step * GROUP_SIZE instead of step on each probe iteration. The for loop over step implements quadratic probing by group.
• Create a crate::sse::Group from a slice of the metadata array starting at the current index. Group represents 16 adjacent metadata entries and is a newtype wrapper around u8x16.
• Use Group::to_candidates to compute a set of candidates—full buckets with an h2 that matches k’s—using SIMD operations. Then, iterate over the candidates to see if any of their keys matches k. If we find a match, return ProbeResult::Full.
• If we haven’t found a match, check our group for empty buckets with Group::to_empties (using SIMD ops) and return ProbeResult::Empty if one is found.
• If we didn’t find any matches or any empty buckets, then the group contains only tombstones and full buckets that don’t match k. Go to the next iteration of the for loop and probe the next metadata group.

Not too bad, right? Next, let’s walk through the implementation of those SIMD routines on Group.

SIMD operations

Since we’ll also use SIMD in sixth::Map, I decided to split it off into a new module, sse.rs:

// sse.rs

//! Defines the group for SSE probing.
use std::simd::{self, SimdPartialEq, ToBitMask};

use crate::metadata;

pub const GROUP_SIZE: usize = 16;
pub type SimdType = simd::u8x16;
pub type MaskType = simd::mask8x16;

// continued...

Above, we defined the GROUP_SIZE of 16 and added some type aliases for convenience.

Group methods

We’ll represent each Group as a newtype wrapper around SimdType (i.e., u8x16):

// sse.rs

#[derive(Clone, Copy)]
pub struct Group(SimdType);

impl Group {
    #[inline]
    pub fn from_slice(s: &[u8]) -> Self {
        Self(SimdType::from_slice(s))
    }

    #[inline]
    pub fn to_empties(self) -> MaskType {
        let empty = SimdType::splat(metadata::empty());
        empty.simd_eq(self.0)
    }

    #[inline]
    pub fn to_candidates(self, h2: u8) -> MaskType {
        let h2 = SimdType::splat(h2);
        h2.simd_eq(self.0)
    }
}

These methods on Group are what we’ll use to test our metadata. The from_slice method just uses Simd::from_slice to create a u8x16.

Both methods to_empties and to_candidates consume the Group and produce a MaskType with 16 boolean lanes (i.e., mask8x16). The true lanes in the output correspond to metadata entries that match the query—empty buckets (for to_empties) or full buckets with matching h2 (for to_candidates). To implement to_empties, we use Simd::splat to initialize metadata::empty() into the lanes of a u8x16 vector, and then take a lane-wise == with the group. To implement to_candidates, we do the same thing but splat the desired h2 instead of metadata::empty().

Checking the generated assembly

Let’s double-check that the compiler is actually emitting SSE instructions as we expect. To do this, we’ll mark Group::to_empties with #[inline(never)] so cargo-show-asm can easily locate it, then run

$ cargo asm --lib "cornedbeef::sse::Group::to_empties"

which outputs

cornedbeef::sse::Group::to_empties:

	.cfi_startproc
	mov rax, rdi

	movdqa xmm0, xmmword ptr [rsi]

	pcmpeqb xmm0, xmmword ptr [rip + .LCPI5_0]

	movdqa xmmword ptr [rdi], xmm0

	ret

Yup—above, we see pcmpeqb, which is a SIMD compare for equality instruction. We’ll ignore the movdqa instructions for now—those are there because we didn’t inline the function. (See Performance Pitfall #1 for more details.)

Mask utilities

Finally, we have a MaskIter utility to iterate over the set bits of a mask:

// sse.rs

pub struct MaskIter<D> {
    inner: u16,
    _direction: D,
}

pub struct Forward;
pub struct Reverse;

impl MaskIter<Forward> {
    #[inline]
    pub fn forward(mask: MaskType) -> Self {
        Self {
            inner: mask.to_bitmask(),
            _direction: Forward,
        }
    }
}

impl MaskIter<Reverse> {
    #[inline]
    pub fn reverse(mask: MaskType) -> Self {
        Self {
            inner: mask.to_bitmask(),
            _direction: Reverse,
        }
    }
}

impl Iterator for MaskIter<Forward> {
    type Item = usize;

    #[inline]
    fn next(&mut self) -> Option<Self::Item> {
        match self.inner.trailing_zeros() as usize {
            GROUP_SIZE => None,
            i => {
                // Unset the i-th bit.
                self.inner ^= 1 << i;
                Some(i)
            }
        }
    }
}

impl Iterator for MaskIter<Reverse> {
    type Item = usize;

    #[inline]
    fn next(&mut self) -> Option<Self::Item> {
        match self.inner.leading_zeros() as usize {
            GROUP_SIZE => None,
            i => {
                let i = 15 - i;
                // Unset the i-th bit.
                self.inner ^= 1 << i;
                Some(i)
            }
        }
    }
}

We use to_bitmask to convert the mask to a u16. To iterate over the set bits, we use either u16::trailing_zeros() or leading_zeros() (depending on the direction we’re iterating). Every time we see a set bit, we unset it before returning its index. This should be pretty fast, as trailing_zeros and leading_zeros use compiler intrinsics under the hood. I wrote this after taking a peek at the BitMaskIter type in hashbrown, which follows a similar approach.

Having done all the hard work in MaskIter, we can also write some super simple functions to get the first or last set bit in the mask:

// sse.rs

/// Find the first set bit in the mask.
#[inline]
pub fn find_first(mask: MaskType) -> Option<usize> {
    MaskIter::forward(mask).next()
}

/// Find the last set bit in the mask.
#[inline]
pub fn find_last(mask: MaskType) -> Option<usize> {
    MaskIter::reverse(mask).next()
}

That’s it for the SIMD code! The next section discusses two performance pitfalls that I encountered when first writing the SIMD routines.

Performance pitfalls

Pitfall #1: std::simd ABI

You probably noticed that I used #[inline] a lot above. This is necessary due to a current limitation in std::simd’s ABI (application binary interface): Simd and Mask function arguments or return values are passed through memory by default, instead of in SIMD registers.

The std::simd docs suggest using #[inline] as a fix, which helps the compiler use SIMD registers instead. I found this to be critical for good performance: using #[inline(never)] instead of #[inline] resulted in about a 70% regression (!) in the insert benchmarks.

To see this in more detail, let’s look at the assembly for Group::to_empties again with inlining turned off:

cornedbeef::sse::Group::to_empties:

	.cfi_startproc
	mov rax, rdi

	movdqa xmm0, xmmword ptr [rsi]

	pcmpeqb xmm0, xmmword ptr [rip + .LCPI5_0]

	movdqa xmmword ptr [rdi], xmm0

	ret

We see that the function is reading and writing from memory (whatever addresses are held in rsi and rdi, respectively), via the movdqa instructions. We expect that this should be a lot slower than passing the vectors in registers and, as mentioned above, this is confirmed by the benchmarks.

Now, let’s look at the “good case” where the function is inlined. When we put the #[inline] attribute back, Group::to_empties gets inlined into Map::probe_find, so we should look at the assembly for Map::probe_find. That turns out to be pretty long, but we can simply grep it for movdq, which only turns up three instructions:

$ cargo asm --lib "cornedbeef::fifth::Map<K,V>::probe_find" | grep movdq

	movdqa xmm1, xmmword ptr [rip + .LCPI3_0]
	movdqu xmm2, xmmword ptr [rcx + rax]
	movdqa xmm3, xmm0

The last instruction is just moving data between SIMD registers, which I’d expect to be very fast. So that leaves us with two reads from memory to SIMD registers. The movdqu is an unaligned SIMD move, which is the conversion from the (unaligned) 16-element slice of self.metadata into a SIMD vector. The other movdqa splats Metadata::empty() into a SIMD vector—since Metadata::empty() is a const fn, this value is just stored as a constant in the code at .LCPI3_0.

This makes it pretty clear why inlining the SIMD functions is so important: Group::from_slice, Group::to_empties, Group::to_candidates, MaskIter::forward, and MaskIter::reverse would probably have used four memory reads/writes each if not inlined!

Pitfall #2: Mask::to_array

I originally tried to implement iteration over the mask by using Mask::to_array to convert the mask8x16 into a [bool; 16] array. Something like this:

// Generate candidates mask and convert to an array.
let candidates = group.to_candidates().to_array();
for (i, m) in candidates.into_iter().enumerate() {
    // If the mask is set, then do something with it.
    if m { 
        // Do stuff with the bucket at `i`...
    }
}

However, I found that this gave about 40% slower performance (!) on the insert_grow benchmarks than the MaskIter design.

My guess is that the current MaskIter design performs better because we always stay in a SIMD register. Similar to not inlining in Pitfall #1, using Mask::to_array ends up writing our SIMD register out to memory. Supporting this, the measured speed hit is also comparable to when we don’t inline the SIMD methods.

Loose ends

Finally, let’s discuss a few more tweaks we need to do to make SIMD probing work.

Metadata double-update

As mentioned earlier, self.metadata now holds an extra copy of the first GROUP_SIZE entries at the end of the array, to make it easy to form a full Group for the last few buckets.

As a result, we need to be sure to update these extra entries to keep all the copies in sync. The simplest way would be to just check if index < GROUP_SIZE, but in the interest of avoiding branches, I copied this trick from hashbrown:

// fifth.rs

impl<K, V> Map<K, V> {
    fn set_metadata(&mut self, index: usize, value: Metadata) {
        let index = fast_rem(index, self.n_buckets());
        let index2 = fast_rem(
            index.wrapping_sub(GROUP_SIZE), 
            self.n_buckets()
        ) + GROUP_SIZE;

        self.metadata[index] = value;
        self.metadata[index2] = value;
    }
}

Note that if index is not in the first or last GROUP_SIZE positions in self.metadata, then index == index2, and we simply write the value twice. This again relies on self.n_buckets() being a power of 2 for the wrapping_sub and fast_rem above to work as intended.

In benchmarking, I didn’t see a massive effect of avoiding the branch, maybe just a few percent effect.

Tombstone complications

Recall that when probing, we only move on to the next group if there are no empty entries in the current group.

This has an interesting implication for the role of tombstones. Suppose we are removing a key, which we’ve found at index i. We only need to place a tombstone if i is inside of a run of GROUP_SIZE non-empty buckets; otherwise, we can just set bucket i back to empty.

Another way of saying this is: we can set i back to empty, unless there exists some group containing i that has no empty buckets (besides i).

Here’s the code, though it’s not particularly interesting:

// fifth.rs

impl<K, V> Map<K, V>
where
    K: PartialEq + Eq + Hash 
{
    /// We can set back to empty unless we're inside a run of `GROUP_SIZE`
    /// non-empty buckets.
    fn decide_tombstone_or_empty(&self, index: usize) -> Metadata {
        // Degenerate case where n_buckets is GROUP_SIZE
        if self.n_buckets() == GROUP_SIZE {
            return metadata::empty();
        }

        let probe_current = sse::Group::from_slice(&self.metadata[index..]);
        let next_empty = sse::find_first(probe_current.to_empties())
            .unwrap_or(GROUP_SIZE);

        let previous = fast_rem(index.wrapping_sub(GROUP_SIZE), self.n_buckets());
        let probe_previous = sse::Group::from_slice(&self.metadata[previous..]);
        let last_empty = sse::find_last(probe_previous.to_empties())
            .unwrap_or(0);

        // Find the distance between nearest two empty buckets.
        // If it's less than GROUP_SIZE, then all groups containing `index` have
        // at least one empty bucket.
        if (next_empty + GROUP_SIZE).saturating_sub(last_empty) < GROUP_SIZE {
            metadata::empty()
        } else {
            metadata::tombstone()
        }
    }
}

likely/unlikely intrinsics and #[cold]

This final tweak is just for performance; it’s not needed for correctness.

Rust exposes some unstable compiler intrinsics through std::intrinsics. In particular, the likely and unlikely intrinsics can be used to tell the compiler which branch in an if statement is likely to be taken. These are used like so:

use std::intrinsics::likely;

if likely(my_likely_condition) {
    // We'll probably go here 
} else {
    // Taking this path is unlikely
}

One place where this could be helpful is in Map::insert. Recall that when inserting, we always have to check first if the map must be resized. However, it’s pretty unlikely that the map actually needs to grow, especially as the n_buckets becomes very large. So we might as well stick an unlikely hint on that branch:

// fifth.rs
impl<K, V> for Map<K, V> {
    pub fn insert(&mut self, k: K, v: V) -> Option<V> {
        if unlikely(self.needs_resize()) {
            self.resize();
        }
        self._insert(k, v)
    }
}

Note that self.resize() is only ever called inside of this unlikely path. Rust also provides a #[cold] attribute to mark functions that are unlikely to be called. So I also decided to slap this onto Map::resize:

// fifth.rs

impl<K, V> for Map<K, V> {
    #[cold]
    #[inline(never)]
    fn resize(&mut self) { 
        // Snip...
    }
}

(Note: to be most effective, #[cold] may need to be used with #[inline(never)].)

The addition of unlikely hints and #[cold] gave a 5-10% speedup on my benchmarks. I have to admit that I was not very scientific about this: I didn’t try to separate the effects of #[cold] and unlikely, so I’m not sure if one or the other was more important.

Speed comparison with std

Here are the final performance results. As always, the numbers shown are ratios with std’s runtime.

Benchmark	fourth	fifth v0	fifth v1	fifth v2
new (capacity: 0)	0.7	0.5	0.5	0.5
new (capacity: 10⁵ 16-byte items)	1.0	1.0	1.0	1.0
drop (10⁵ items)	1.03	0.95	1.00	1.03
insert_grow_seq (payload: 8 bytes)	1.79	1.47	1.46	1.32
insert_grow_seq (64 bytes)	1.69	1.49	1.35	1.26
insert_grow_random (8 bytes)	1.83	1.51	1.42	1.38
insert_grow_random (64 bytes)	1.69	1.45	1.36	1.28
insert_reserved_random (8 bytes)	1.43	1.24	1.14	1.05
insert_reserved_random (64 bytes)	1.38	1.38	1.15	1.08
lookup (8 bytes)	1.24	1.23	1.23	1.27
lookup (64 bytes)	1.24	1.52	1.34	1.39
lookup_string (8 bytes)	0.94	1.06	1.12	1.17
lookup_string (64 bytes)	0.99	0.93	1.07	1.07
lookup_miss (8 bytes)	1.61	1.11	1.11	1.05
lookup_miss (64 bytes)	1.50	1.00	1.10	1.15
remove (8 bytes)	0.84	1.03	1.00	1.06
remove (64 bytes)	0.96	1.13	1.12	1.14

As you can see from the table, for the fastest version (v2), we are about 30-40% slower than std::collections::HashMap for most operations, and almost as fast as std for insert_reserved, lookup_miss, and remove.

The labels “v0” etc. are shorthand for the following:

• v0: just adding SIMD probing.
• v1: addition of likely/unlikely and #[cold]
• v2: liberally using get_unchecked to remove bounds checks

The main branch of the repo is currently at v1.

I put v2 in a separate branch (here); I decided not to merge this into main since all of the extra unsafe is a little ugly. With more effort, we could probably also get rid of the bounds checks more safely (for some options, see How to avoid bounds checks in Rust (without unsafe!)).

Next steps: Allocator API

In the beginning of this series, I promised a sixth and final version of the map using Rust’s Allocator API to put the metadata and storage arrays in the same allocation. Sadly, I am going to break this promise for now…

I have some code that does this, although it’s not yet using the SIMD probing from this post. Feel free to check out it out in mod sixth in the repo. Though it’s passing my limited set of miri tests, I’m sure that the implementation is quite unsound. I’m excited about making it fully safe, but not sure if I’ll take the time to fully write it up.

I may come back to this eventually, but in the meantime I would recommend checking out hashbrown, which has a lot of excellent comments explaining the important safety considerations.

Footnotes